Keras 損失函數

選擇模型類別後，我們就要針對要解決的問題，決定要最小化甚麼目標函數，即損失函數(loss function)，常用的損失函數如下：

1. 均方誤差(mean_squared_error)：就是我們之前講的最小平方法(Least Square) 的目標函數 — 預測值與實際值的差距之平均值。還有其他變形的函數, 如 mean_absolute_error、mean_absolute_percentage_error、mean_squared_logarithmic_error。
   
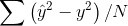
2. Hinge Error (hinge)：是一種單邊誤差，不考慮負值，適用於『支援向量機』(SVM)的最大間隔分類法(maximum-margin classification)，詳細請參考 https://en.wikipedia.org/wiki/Hinge_loss。同樣也有多種變形，squared_hinge、categorical_hinge 。
   
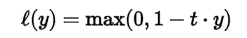
3. Cross Entropy (categorical_crossentropy)：當預測值與實際值愈相近，損失函數就愈小，反之差距很大，就會更影響損失函數的值，這篇文章 主張要用 Cross Entropy 取代 MSE，因為，在梯度下時，Cross Entropy 計算速度較快，其他變形包括 sparse_categorical_crossentropy、binary_crossentropy。
   
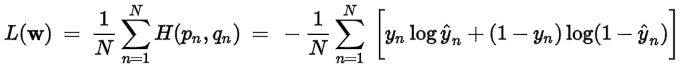
4. 其他還有 logcosh、kullback_leibler_divergence、poisson、cosine_proximity 等。
5. 注意! 損失函數、Activation Function 不限使用現成的函數，也可以自訂函數，尤其是損失函數，我們常需要自訂，例如目標函數為庫存成本，我們通常要最小化，但是，如果我們應用在銷售系統上，要極大化銷貨利益，假設庫存短缺造成無法接單，所減少的收益(L1)是兩倍於庫存的儲藏成本(L2)，損失函數就應該訂為 L1 * 2 + L2。另外，我們的目標可能是『最大化』收益，而非最小化損失，我們就必須對變數作一些轉換，使函數變為『最小化”負”收益』，因為，Keras優化都是『最小化』(Minimize)求解，沒有最大化(Maximize)。後續介紹『風格轉換』(Style Transfer)，將照片轉成不同畫風的程式，就是一個典型的例子，它為畫風(Style)定義了一個特殊的函數。